The finite element method is a widely used technique in physical computing. Obtaining more accurate results with less computational cost is a goal pursued by many industries. The CAD&CG State Key Laboratory of Zhejiang University has improved the performance of non-uniform and nonlinear elastic deformation simulation by several orders of magnitude by designing a new finite element shape function.
Recently, Prof. Bao Hujun, Prof. Huang Jin, Chen Jiong, a PhD student and Wang Tianyu, a master student from the CAD & CG State Key Laboratory of Zhejiang University collaborated with Prof. Mathieu Desbrun from the California Institute of Technology. The team proposed a numerical homogenization method based on discontinuous shape functions.
This method meticulously designed a matrix-form, piecewise linear shape function that can perceive some of the deformation characteristics induced by heterogeneous materials. This offers a better approach to compute grids and effectively increased the order of magnitude of finite element calculations.
This research finding is published in top computer graphics conference SIGGRAPH 2018. It proposed a method for solving a problem-related discontinuous matrix shape function on a coarse grid. Compared to directly solving on a precise grid, this method enhances performance by 1000 times, and also surpassed previous methods in terms of simulation accuracy and range of application.
Feature 1: Matrix Shape Function Capable of Sensing Heterogeneous Materials
Efficient simulation of complex and nonlinear elastic deformation is of great significance in mechanical analysis. With the ever-increasing complexity and enormous simulation demand, finding a highly efficient numerical method with linear scaling of problem complexity versus time cost has become a major technical problem. In engineering, one can only use sufficiently fine grids to approximate non-uniform deformations on the microscale so as to retain as much detail as possible. However, if the simulated object is very complex geometrically, this fine-grained discrete dissection can make the computational cost unacceptable. Typical examples include the vein structure on an organ or microstructure of 3D printing element materials.
The main purpose of Prof. Bao Hujun and Prof. Huang Jin’s research is to accelerate finite element calculations and thereby improve the efficiency of physical simulation in film, aviation, machinery and civil engineering. The finite element method has been proposed since the 1960s, and has been continuously improved by numerous scholars throughout the years. However, little attention has been paid to reconstructing the shape functions used in the elastic equation.
The team discovered that the traditional scalar shape function has certain limitations and cannot reflect the coupling relationship between the various directions of an object. This is inconsistent with the anisotropic deformation characteristics caused by the complex heterogeneous materials. Therefore, this study extended the scalar basis function to a matrix basis function determined by materials and boundary conditions. The matrix basis function itself is expressed as a combination of piecewise linear functions, thereby making the construction of the basis function a problem that can be separately solved.
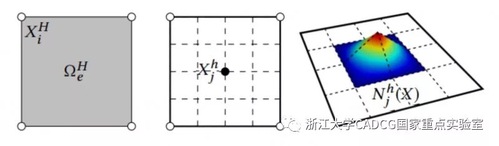
Figure 1: A coarse-grid unit in two-dimensional case (left) and its associated fine-grid unit and vertices (middle plot). Each fine-grid vertex is associated with a local basis function, defined by its associated fine-grid unit.

Figure 2: Comparison between the traditional finite element method and the new method
The numerical homogenization method proposed by the team demonstrated good calculation efficiency and accuracy. From Figure 2, we can see that the simulation result obtained by using the optimized shape function (red) is closer to the real solution (blue) on the fine grid than the result obtained by the traditional finite element shape function (green).

Figure 3: The upper graph (left) is the result of a fine grid, calculated using the traditional method; the upper graph (right) is the result of the new method proposed by the team.
Figure 3 shows the results of using this method to compute a hand playing piano versus the traditional method. It can be seen that on geometric objects with more detailed features, similar results can be obtained with fine grids using new shape functions.
The ratio of the number of fine grid cells to coarse grid cells in the result is 8:1. The following figure shows the computing time comparison. The new method only used 1/60 of the time of the traditional method. When the ratio of the number of fine grid cells to coarse grid cells is 64:1, the method can be faster by over a thousand times.

Figure 4: the red line is the convergence time of the new method and the blue line is the convergence time of traditional method.
Apart from the fact that the method can obtain a good approximation of heterogeneous materials, it also maintains decent consistency with stress distribution on coarse and fine grids. Therefore, in addition to some visual effect-based application scenarios such as movies, animations and interactive designs, this method also has great application potential in fields such as civil engineering and manufacturing.

Figure 5: In each chart, the left figure represents the traditional method and the right figure represents the new method proposed by Prof. Bao Hujun and Prof. Huang Jin’s team.






